| Vampire |
Posted - Aug 09 2005 : 04:00:57 AM
I succeeded to load a 3ds file in my project. But lights didn't work on it's meshes. Yeah. I put normals and it worked.
BUT!
The lighting of the faces wasn't smooth. I mean no gradient. The face was totally lit or totally shaded. It looks ok for a special effect but not all the time. I thought, the generated normals are my problem.
So I worked out to load a Milkshape ASCII .txt file in the project. This format has the normals specified (no generation needed). Bu the result is just the same.
Who's fault is this? The lights', the normals', the material's or mine? |
| Eric Coleman |
Posted - Aug 10 2005 : 11:53:54 AM
Yes, that would work. However, you may want to apply a weight to each vertex depending on the percentage of the angle it creates at a particular joint.
2 Examples in this picture.
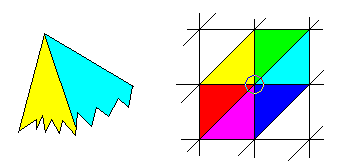 
For the first example, the point at the top of the yellow and cyan triangles would simply be an average between them. However, you may want to give more weight to an angle depending on how much surface area it provides to a common vertex location. For this case it would be the following equation:
N = (Theta_y / (Theta_y + Theta_c)) * N_y + (Theta_c / (Theta_y+Theta_c)) * N_c
Theta_y and Theta_c are the angles made by the Yellow and Cyan triangles.
N_y and N_c are the normals for the Yellow and Cyan triangles
For the second example, you stll need to calculate the individual angles for each triangles. In a clockwise direction, starting from green, you have the following colors, green, cyan, blue, purple(magenta), red, and yellow.
Don't make the mistake of assuming that the sum of their angles = 360 degrees. If the angles are all flat, then their normals will all be same and you don't even need to calculate the normals. However, if you're drawing terrain, which is hardly ever flat, then you'll need to have a weighted calculation.
Here is the equation that you'll need to use for this case:
Theta_sum = Theta_g + Theta_c + Theta_b + Theta_p + Theta_r + Theta_y
N = Theta_g / Theta_sum * N_g + Theta_ c/ Theta_sum * N_c + Theta_b / Theta_sum * N_b + Theta_p / Theta_sum * N_p + Theta_r / Theta_sum * N_r + Theta_y / Theta_sum * N_y
You can make things even more complicated by weighing the surface area of a triangle as well. And you don't have to have a linear weight either. You could use a sine curve or whatever you want for blending the normals between adjacent triangles.
Of course, you only really need to do this once when loading the data or even precalculate it and save it in your own format. For geometry that changes, then you'll probably want to recacluate the normals based on the new positions, but depending on the situation, it shouldn't occur that often. If an explosion blows a hole in your terrain, then you only need to recalculate the modified vertices and not the whole map. |
| Vampire |
Posted - Aug 09 2005 : 11:52:20 PM
And how should I do that?
Like this is ok?
I take each triangle in a smoothing group. I look at their vertices and if I find a vertex in more than one triangle, I blend it's normals.
purplenormal.x = (bluenormal.x + rednormal.x) / 2
purplenormal.y = (bluenormal.y + rednormal.y) / 2
purplenormal.z = (bluenormal.z + rednormal.z) / 2
I hope, I need to do that only at loading and not in every frame, real-time.
I'll try it right now, but if you know that it won't work, please give me a solution. (I don't have the patience to look for a tutorial over the net  ) ) |
| Eric Coleman |
Posted - Aug 09 2005 : 09:46:59 AM
The problem is the normals aren't smooth between the faces. In most 3D drawing applications you have "smoothing groups", which allow you to blend the normals between faces of polygons.
There are many different methods to accomplish this, but the idea is simple. For adjacent polygons blend them together so that they're the same.
Look at this picture...
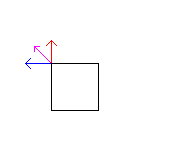
The blue normal is for the vertex of the polygon on the left side, the red normal is for the vertex of the polygon on the top side. Blend them together however you want, and then use the blended purple normal for both vertices.
|
|
|