|
General:
Matrix Maths
Author:
Jack Hoxley
Written: 12th July 2001
Contact: [EMail]
Contents
of this lesson
1. Introduction
2. 2D Transformations
3. 3D Transformations
1.
Introduction
I've
had so many emails in recent months about the
transformation of 2D and 3D geometry that I'm
getting bored with it - so I thought, to answer
the question for the final time, I'll write an
article to explain the whole thing. This is that
article...
Transformation
consists of 3 things - rotating (spinning things
around), scaling (making things bigger/smaller)
and translation (moving things around). With 3D
graphics Direct3D will do 99% of the work for
you, however, along my travels I've found a way
of going faster - if you do the matrix maths calculations
yourself you can go just that little bit faster
(2.5x faster), we're talking the difference between
0.0001ms and 0.00005ms here, but if you're rendering
500+ objects a frame (several 1000 a second),
it could be worth the extra effort. It also looks
much cleverer! (if you open-source your code).
Onwards
and upwards...
2.
2D Transformations
This
is the most useful part, using either DirectDraw
(fully 2D) or Direct3D (quasi 2D) no transformations
are done for you - you want to rotate, translate
or scale something you're gonna have to do it
yourself. The actual mathematical proof behind
all of this is a little complicated, and to be
honest - it really makes much difference why it
works, all we want to know is how to make it work
for us. Much of the pure maths is glossed over
here, if you're interested in proofs or further
explanations dig out your old maths books or go
searching the web - much of the pure maths is
too lengthy to explain here.
We're
going to be using a mathematical technique known
as matrix maths - the ideas behind matrices (plural
of matrix) isn't too important, heck! I dont even
know exactly how to use them - I just learnt what
I need to know about them. Matrix maths allows
us to do the transformations relatively quickly,
and relatively simply as well - just what I like.
The
basic structure is like this [X,Y] ---} [M] ---}
[X',Y'] (one set of coordinates goes in, something
happens, and a new set of coordinates come out).
[M] is the transformation matrix, it may scale
the coordinates, rotate them, translate them or
some combination of the 3. The best part is that
you can combine all 3 transformations into one
matrix (more on that later).
Translation
This is probably the easiest of the 3, and
thus we'll start here. A 2D translation matrix
for what we want is a 3x3 grid of numbers (known
as a 3x3 matrix). for a translation it looks like
this:
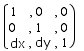
a
bit weird really, isn't it. in order to translate
a point by this matrix we must multiply the point
by the matrix. Now this isn't as simple as it
sounds, it's not quite like normal multiplication,
and it's an awful lot more complicated. if we
refer to all of the elements in row-column notation
(ie, yx) and the rows are i and columns j, to
get the FINAL value for element <i,j> we
multiply each element in the row i (of the source
matrix) with each element in the column j (of
the destination matrix), we then add all of these
values together and that is our final value. scared?
look at this following example and see if you
can understand what happened:
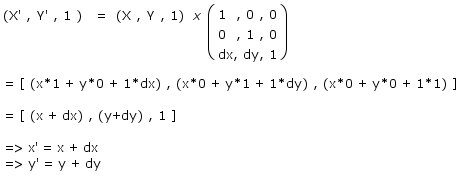
it
aint too scary really, is it? the final results
aren't particularly amazing - I'm pretty sure
that without all this extra work you could of
told me how to translate the original coordinates
(the x' = x + dx part)... It'll come into it's
own a little later on when we're combining rotation,
scaling and translation into one big equation.
Rotation
Rotation is the big one - this is what everyone
likes emailing me about. Rotating your sprite
around is a very useful trick in games - and is
often quite heavily used; therefore it obviously
helps being able to do it! The following diagram
shows you what the 2D rotation matrix should look
like:
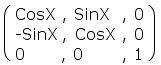
A
little more scary this time - trig functions.
The presence of these trig functions will bring
the processing time for a rotation transformation
up considerably - trig functions are slow. If
you can optimise away any of the trig functions
then do so - the only realistic optimisation to
be done here is to pre-process CosX and SinX,
as that will 1/2 the number of calls to Cos( )
or Sin( ). More on this later (when we do a bit
of code).
I've
already explained the basics of matrix multiplication
in the translation section, so it should
make sense this time around - if not, the derived
equations are perfectly usable without any knowledge
of matrix mathematics. Here's how we rotate our
point [x,y] by X radians to retrieve [x',y'] :
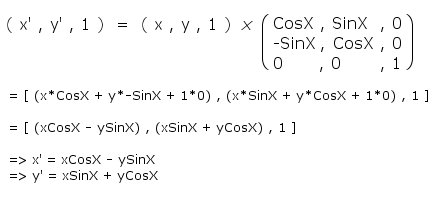
Again,
not too simple if you can see your way through
the matrix multiplication algorithm. Be careful
to differentiate between the X and the x, the
X is the angle (usually denoted as theta, q),
and x is the coordinate.
Scaling
This isn't used as often, but it's pretty
simple - so I may as well explain it, and we can
incorporate it into the big matrix later on. You
may have noticed that all of the matrices so far
have had the r=c values equal to 1 (unless replaced
by another value), this is because the r=c values
are the scaling values - in previous matrices
they are set to 1 so that they dont intefere with
the resultant values. a matrix where all the values
are 0 except the r=c values which are 1 is called
the "identity matrix", which is a useful
type of matrix, but not really relevant here.

Not
at all complicated, and neither is the resulting
equations - you can probably guess them now!
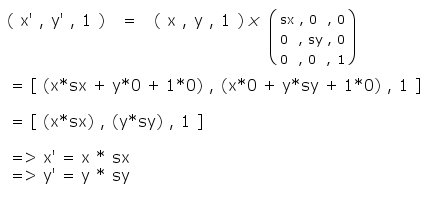
Tell
me you could see that coming? it's pretty obvious...
Combining
Transformations
Up till this point, the use of matrices has been
a little pointless - the derived equations are
enough to rotate, translate and scale. you could
quite easily apply each transformation individually
like this:
x'
= x + dx
y' = y + dy
x'' = x'Cosq - y'Sinq
y'' = x'Sinq + y'Cosq
x''' = x'' * sx
y''' = y'' * sy
the
above code would translate the point, rotate it
around the origin and then scale it by a given
factor - not necessarily what you want (rotation
before translation is more common), but you can
juggle the lines around. BUT, using matrices we
can combine all 3 transformations together, then
split them out into two lines - generating x',y'
from x,y instead of going all the way to x''',y'''
- is that not better?
The
way we do this is by creating a master matrix
- we multiply (using matrix multiplication) the
translation, rotation and scaling matrices together
into one matrix, then multiply the point x,y by
this master matrix. A prior note on multiplication
order - as with the 6 equations just listed it
matter what order they go in, rotation-translation
is very different from translation-rotation (one
will create an orbiting body, the other will create
a spinning object). Normally you would scale the
points, rotate them and then translate them -
but you'll need to decide which is best for your
application. here is the complete proof for the
"master matrix":
[M]
is the Master Matrix
[S] is the scaling Matrix
[R] is the rotation Matrix
[T] is the translation Matrix
[M]
= [S][R][T]
= ( [S]*[R] ) * [T]
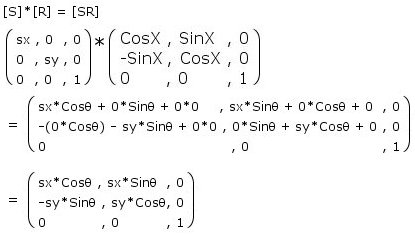
[M]
= [SR][T]

there
we have the final "Master Matrix". How
amazing, if we now multiply a point [x,y,1] by
this matrix we should be left with an equation
to transform x and an equation to transform y
- which will result in a rotation, translation
and scaling. Arguably, through substitution, you
could of combined the original 3 equations, but
this way is open to much more powerful calculations
- there are quite a few other types of transformation
that can be done using matrices, and a few shortcuts
can be found along the way as well. The following
illustration indicates how the final all-in-one
formula works:
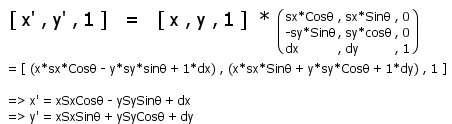
So
the final equation to transform the point (x,y)
- rotating through q radians, scaling by (sx,sy)
and translating by (dx,dy) units - is shown above.
we can prove that this combined equation is actually
correct by substituting in the previous set of
equations - shown below.
Scale:
x' = x * sx
y' = y * sy
Rotate:
x'' = x'Cosq - y'Sinq
y'' = x'Sinq + y'Cosq
Translate:
x''' = x'' + dx
y''' = y'' + dy
Combined:
x' = ((x * sx)Cosq
- (y * sy)Sinq) + dx
y' = ((x * sx)Sinq
+ (y * sy)Cosq) + dy
Simplified:
x' = xSxCosq - ySySinq
+ dx
y' = xSxSinq + ySyCosq
+ dy
and
there, as if by magic - we've gotten the same
formula back. The method you choose - by straight
algebra or by matrix algebra - is your choice
entirely; I personally prefer the matrix method
as it allows for many 1000's of combinations;
for example - scale, rotate, translate, rotate
- will (given a flying saucer object) spin it
around it's center and then spin it around the
origin (like orbiting a planet) - you try doing
that with those plain equations, it's still possible
- but a little more complicated methinks. To finish
things off, I've written a simple transformation
function incorporating the overall equation.
Private Function Transform2DPoint(tX As Single, tY As Single, sX As Single, sY As Single, Theta As Single, SrcPt As Pt) As Pt
'(tX,tY) describes the translation
'(sX,sY) describes the scale
'Theta describes the rotation
'SrcPt is the point to be transformed
'[RETURN] is the transformed point
' The general formulas:
' X' = xSxCosq - ySySinq + dx
' Y' = xSxSinq + ySyCosq + dy
Dim Cosq As Single
Dim Sinq As Single
Cosq = Cos(Theta)
Sinq = Sin(Theta)
Transform2DPoint.X = (SrcPt.X * sX * Cosq) - (SrcPt.Y * sY * Sinq) + tX
Transform2DPoint.Y = (SrcPt.X * sX * Sinq) + (SrcPt.Y * sY * Cosq) + tY
End Function
|
|
|
|
3.
3D Transformations
I'm
not going to say much on this topic - 90% of what
was in the previous section is still relevant
in this section. More importantly, however, is
that Direct3D (or any other 3D API) will do matrix
transformations for you - only the specialist/elite
will need to play around with the transformation
matrices manually.
The
advantage of having D3D do the actual transformation
is that all you need to do is present the overall
matrix and it'll work out what needs to happen
- and in some cases the hardware will actually
do the mathematics on the geometry (which is going
to be 10000x faster than any software implementation).
As visitors to the VoodooVB message board will
be aware, I actually worked this out a while back
and posted a generalised matrix formula for a
3D transformation. During my tests on this it
gave exactly the same results as using the built
in D3DX functions, yet was 1.6-2.6x faster than
them. The only trade off is actually working out
the generalised matrix in the first place - this
usually only ever has to be done once.
The
only two differences between the 2D matrices and
the 3D matrices is their size (now 4x4 instead
of 3x3) and there are 3 rotation matrices (x,y,z)
- 2D rotation (on a plane) only requires you to
have 1 rotation axis, 3D has 3 main rotation axis's...
The
5 matrices are shown below - this is for reference,
given the information about 2D transformations
you should quite easily be able to do some clever
things with them...
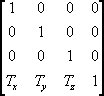 -
- 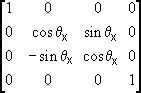 -
- 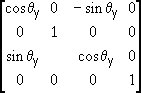
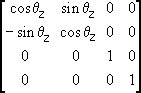 -
- 
Finally,
As I already mentioned, I calculated the generalised
matrix for this a while back - and it's shown
below.
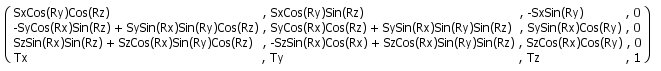
Pretty
isn't it! Here's the same transformation matrix
but in code:
|
Private
Function CreateMatrix(Rx
As Single, Ry As Single,
Rz As Single, Sx As
Single, _
Sy As Single, Sz As
Single, Tx As Single,
Ty As Single, Tz As
Single) As D3DMATRIX
Dim
CosRx As Single, CosRy
As Single, CosRz As
Single
Dim SinRx As Single,
SinRy As Single, SinRz
As Single
CosRx
= Cos(Rx) 'Used 6x
CosRy = Cos(Ry) 'Used
4x
CosRz = Cos(Rz) 'Used
4x
SinRx = Sin(Rx) 'Used
5x
SinRy = Sin(Ry) 'Used
5x
SinRz = Sin(Rz) 'Used
5x
'total of 29 trig
functions
'23 trig functions
cancelled out by
'this optimisation;
hence the 2.6x speed
increase.
With
CreateMatrix
.m11 = (Sx * CosRy
* CosRz)
.m12 = (Sx * CosRy
* SinRz)
.m13 = -(Sx * SinRy)
.m21 = -(Sy * CosRx
* SinRz) + (Sy * SinRx
* SinRy * CosRz)
.m22 = (Sy * CosRx
* CosRz) + (Sy * SinRx
* SinRy * SinRz)
.m23 = (Sy * SinRx
* CosRy)
.m31 = (Sz * SinRx
* SinRz) + (Sz * CosRx
* SinRy * CosRz)
.m32 = -(Sz * SinRx
* CosRx) + (Sz * CosRx
* SinRy * SinRz)
.m33 = (Sz * CosRx
* CosRy)
.m41 = Tx
.m42 = Ty
.m43 = Tz
.m44 = 1#
End With
End Function
|
|
|
|
Conclusion
Wow
- that's a lot of maths, I sure hope someone out
there finds all this useful!! either way, I'm
sure the 2D-Transformation parts will be interesting
for a lot of people. Enjoy!
|